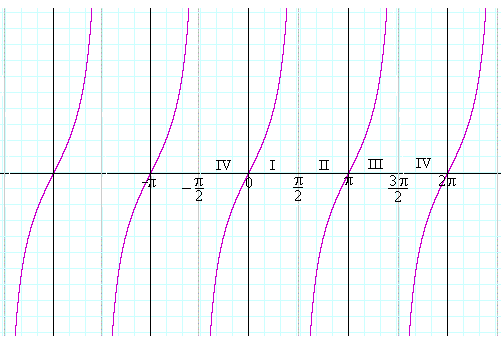
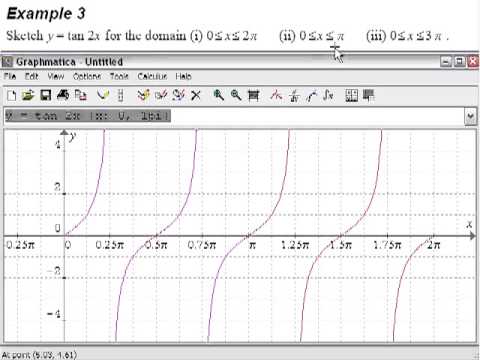
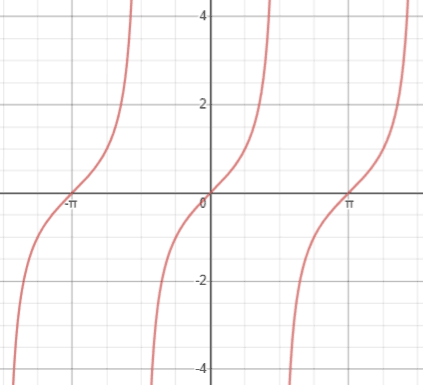
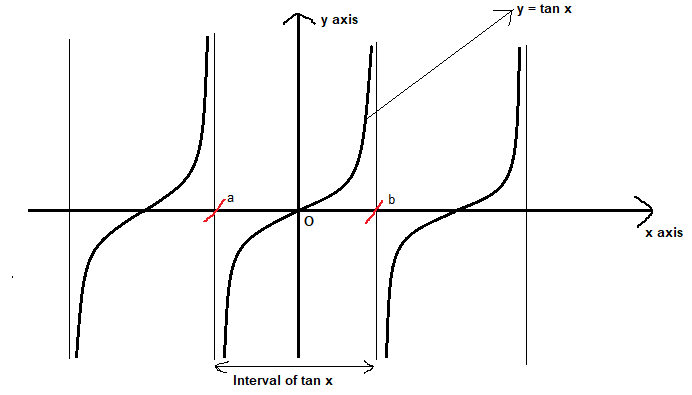
From the graph of the function, we can see that we should be expecting two solutions one solution between 180° and 270° and the other between 270° and 360° \\sin x^\circ = 0349\Multiply the numerator by the reciprocal of the denominator π ⋅ 2 π ⋅ 2 Move 2 2 to the left of π π 2 π 2 π 2 π 2 π The vertical asymptotes for y = tan ( x 2) y = tan ( x 2) occur at − π π, π π, and every 2 π n 2 π n, where n n is an integer x = π 2 π n x = π 2 π n TangentPlot the points and join with a smooth curve Example The diagram shows a graph of y = tan x for 0˚ ≤ x ≤ 360˚, determine the values of p, q and r Solution We know that for a tangent graph, tan θ = 1 when θ= 45˚ and 225˚So, b = 45˚ We know that for a tangent graph, tan θ = 0 when θ= 0˚, 180˚ and 360˚So, c = 180˚ Graphing the Tangent Function

Graphing Tangent Read Trigonometry Ck 12 Foundation
How to graph the tan function
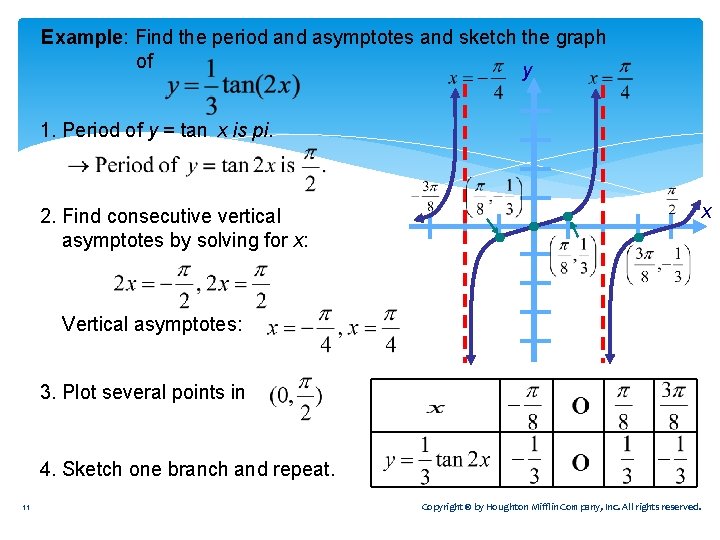
How to graph the tan function-Trigonometric graphs Higher This circle has the centre at the origin and a radius of 1 unit The point P can move around the circumference of the circleMultiply 2 2 by 2 2 x = π 4 x = π 4 x = π 4 x = π 4 x = π 4 x = π 4 The basic period for y = tan ( 2 x) y = tan ( 2 x) will occur at ( − π 4, π 4) ( π 4, π 4), where − π 4 π 4 and π 4 π 4 are vertical asymptotes ( − π 4, π 4) ( π 4, π 4) The absolute value is the distance between a


Graphs Of Trigonometric Functions
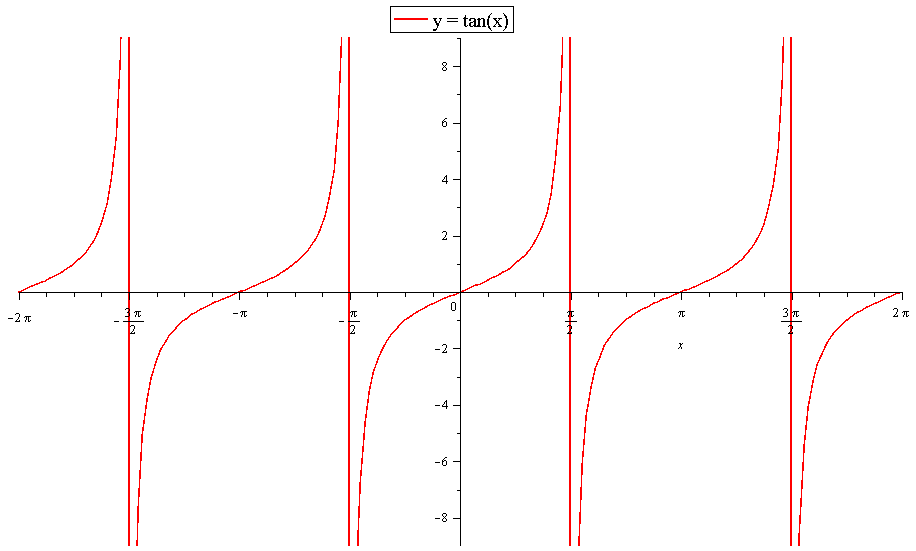
That is not 360 degrees as you might suppose tan x repeats every 180 degrees it's normal period is therefore 180 degrees the period is determined by the normal period divided by the frequency that would make tan(2x) period equal to 180/2 = 90 degrees below is a graph of tan(x) those vertical lines are at 90 degrees (pi/2) and 270 degrees (3pi/2) that's a period of 180 degrees (pi)`tan^2 x=3tanx` To start, subtract both sides by 3tanx `tan^2x3tanx=0` Factor left side `tanx(tanx3) = 0` Set each factor to zero and solve for xThen, locate the number that is located in the same row as 35 degrees and the same column as the 'Tangent' title Using this strategy and the table above, here is what the tangent of a few selected angles is equal to Tangent(4 degrees) = Tangent(31 degrees) = Tangent(45 degrees) = 1 Tangent(70 degrees) = Tangent(25
Jun 14, 16 · Which are the solutions to 8cos^2 theta3cos theta=0, 0 degrees is less than or equal to theta which is less than or equal to 180 degrees ?Type in any function derivative to get the solution, steps and graph This website uses cookies to ensure you get the best experience Decimal to Fraction Fraction to Decimal Radians to Degrees Degrees to Radians Hexadecimal Scientific (tan^{2}x\right) en Related Symbolab blog posts High School Math Solutions – Derivative CalculatorThe below trigonometric tan table lists the corresponding tangent values for the given angle from 0 to 360 degrees, with a precision of 6 decimal digits For example, for the given angle of 23 degrees, the corresponding tangent value would be This tangent values table is helpful to evaluate and simplify the trigonometric tan functions
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreTherefore, we can remove the 180 degrees from the equation {eq}y = 3 tan(2x) \\ {/eq} We also know that tan(x) = tan(x) So, tan(x) = tan(x)Tangent definition In a right triangle ABC the tangent of α, tan(α) is defined as the ratio betwween the side opposite to angle α and the side adjacent to the angle α tan α = a / b Example a = 3" b = 4" tan α = a / b = 3 / 4 = 075 Graph of tangent TBD


6 Trigonometry Graph Example 3 Sketch Y Tan 2x Youtube


Is Tan X A Continous Function Quora
Select all that apply a)00 degrees b)2 degrees c)5 degrees** d)680 degrees e)900 Trigonometry 4 Find the exact value for sin(xy) if sinx=4/5 and cos y =Decimal to Fraction Fraction to Decimal Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Trigonometric Identities Prove (sec^4xsec^2x) = (tan^4xtan^2x)Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel knowledge and


Tangent



Aim What Are The Graphs Of Tangent Function And Reciprocal Functions Ppt Download
Tan(x) degrees radians90°π/2 not defined60°π/°π/4130°π/ 0° 0 0 30° π/6 45° π/4 1 60° π/3 90° π/2 notTan (90θ )=Cot θ;Introduction to Tan double angle formula let's look at trigonometric formulae also called as the double angle formulae having double angles Derive Double Angle Formulae for Tan 2 Theta \(Tan 2x =\frac{2tan x}{1tan^{2}x} \) let's recall the addition formula


Review Cocalc


Math Scene Trigonometry Functions Graphs Of Trig Functions Lesson 3
ORX) tan(2x) The period is and the graph is decreasing on 4 Ox) =tan(2x) The period is and the graph is increasing on Onton() The period is 2x and the graph is decreasing on (4, 5) (b) nn Omcd) The period is 8x and the graph has vertical asymptotes at multiples of 4* OX) The period is and the graph has vertical asymptotes atTo supply an angle to TAN in degrees, multiply the angle by PI()/180 or use the RADIANS function to convert to radians For example, to get the TAN of 60 degrees, you can use either formula below = TAN ( 60 * PI () / 180 ) = TAN ( RADIANS ( 60 ))ATAN2(y, x) returns the arc tangent of the two numbers x and y It is similar to calculating the arc tangent of y / x, except that the signs of both arguments are used to determine the quadrant of the result The result is an angle expressed in radians To convert from radians to degrees, use the DEGREES function


Chapter 7 Trigonometric Functions The Sine Function Imagine
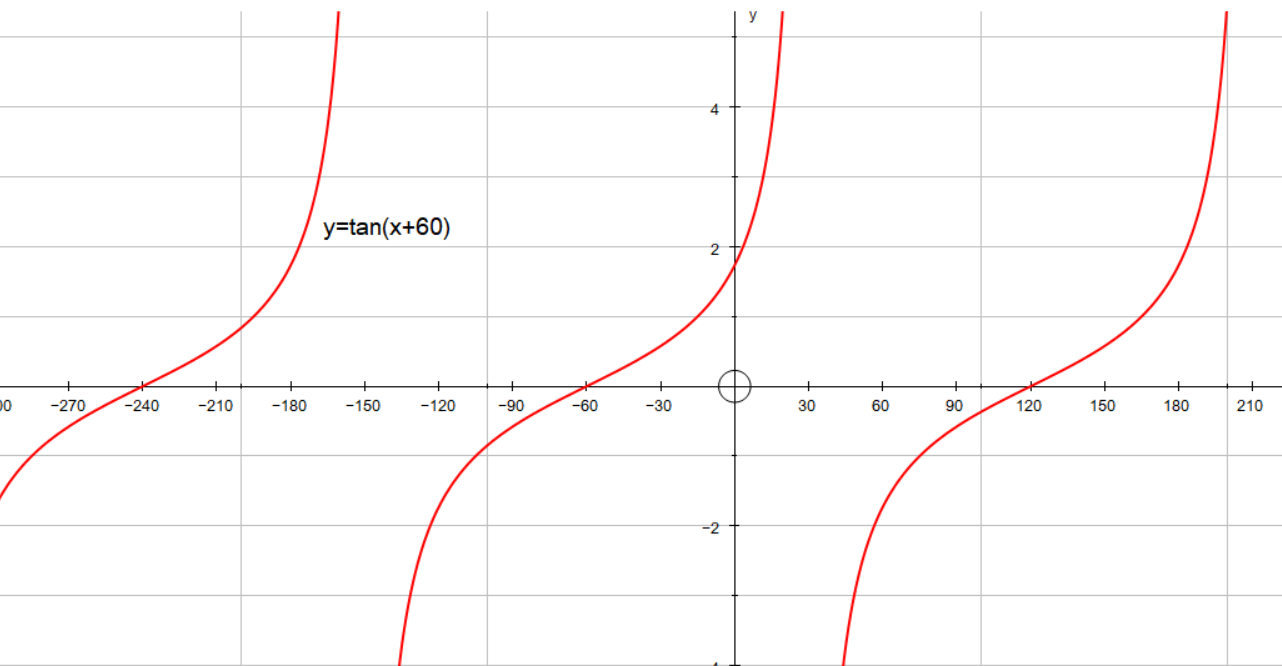


How Do You Graph And List The Amplitude Period Phase Shift For Y Tan X 60 Socratic
The red graph, again, is the standard y = tan x graph The red graph has a phase shift applied to it The only difference between the equations of the two graphs is the value of C is 45 Given an equation y = A tan B (x C) , the value of C dictates the phase shift Note that the standard equation has a negative signWe can use what we know about the properties of the tangent function to quickly sketch a graph of any stretched and/or compressed tangent function of the formlatex\,f\left(x\right)=A\mathrm{tan}\left(Bx\right)\,/latexWe focus on a single period of the function including the origin, because the periodic property enables us to extend theFrom what I know about the graph of the tangent, I know that the tangent will equal 1 at 45° after every 180° These solutions for tan( x /2) are at 0° 45°, 180° 45°, 360° 45° , and so forth
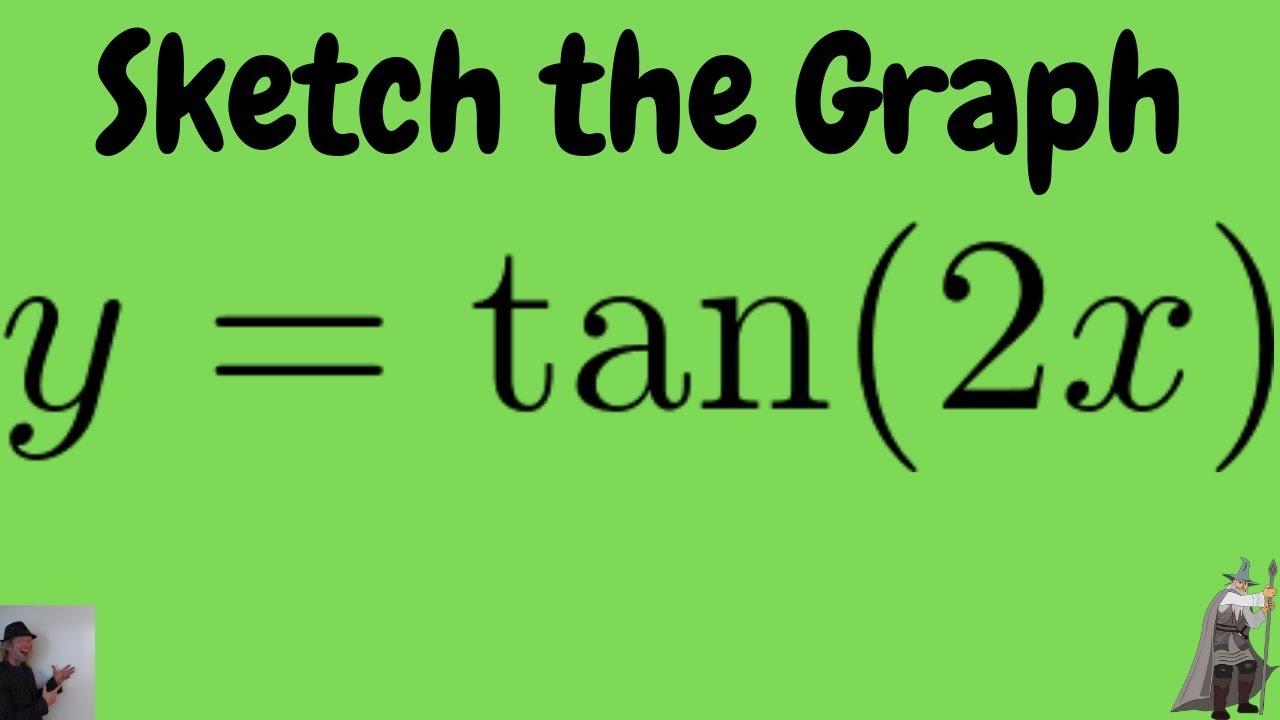


Sketch The Graph Of F X Tan 2x Youtube


Review Cocalc
This implies that graph of cotangent function is the same as shifting the graph of the tangent function 90 degrees to the right Graphic Representations related to tan(90x)=cot(x) Algebraic Proof tan(90x)=cot(x) Powered by Create your own unique website with customizable templatesGraphs Graphing the tangent function using the graphing utility is helpful in finding the critical points, slope, asymptotes, and other vital information, visuallyNov 14, 13 · Find all the angles between 0 degrees and 360 degrees which satisfy the equations a 8 cos x sin x = sin x b 5 tan^2 y 5 tan y = 2 sec^2 y Math Determine each tangent ratio to four decimal places using a calculator A) tan 74 degrees B) tan 45 degrees C) tan 60 degrees D) tan degrees How do I figure this out !?


What Is The Graph Of Mod Of Tan X Quora


Math Scene Trigonometry Functions Graphs Of Trig Functions Lesson 3
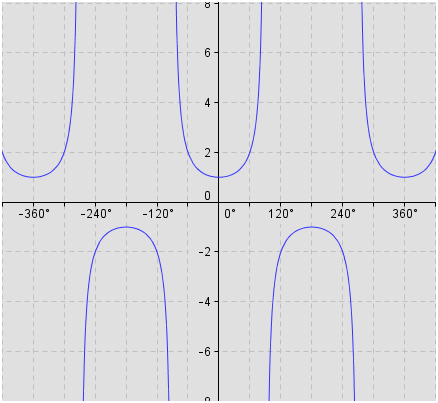
Jun 28, 14 · so what I hope to do in this video is get some familiarity with the graph of tangent tangent of theta and to do that I'll set up a little unit circle so that we can visualize what the tangent of various Thetas are so let's say that's a yaxis this is my xaxis that is my xaxis and the unit circle would look something something like this and we already know this is all of a refresherTan 3x= 3tan xtan 3 x/13 tan 2 x;May 08, 16 · Here's the graph (mousewheel to zoom) graph{tan(2x) 5, 5, 25, 25} The graph is just like tan(x), but 2 times faster It has period pi/2 The roots are at npi/2 for all integers n and graph has slope 2 at these points The asymptotes are at (n1/2)pi/2 More info here


Math Scene Trigonometry Functions Graphs Of Trig Functions Lesson 3



Howto How To Find Vertical Asymptotes Of Tan2x
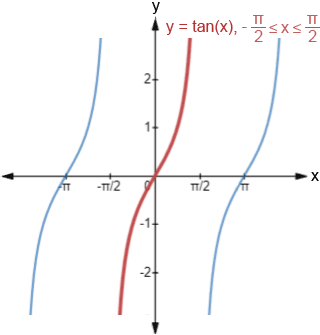
Dec 23, 17 · How do you graph #y=ln(tan^2 x)#?That is, if the point (x, y) lies on the graph of y = tan x so will the point (x kπ , y) where k is any integer Graphing y = sec x, y = csc x, and y = cot x Recall that the secant, cosecant, and cotangent functions are the reciprocals of the cosine, sine, and tangent functions, respectively You are less likely to encounter these graphs inExamining the graph of tan(x), shown below, we note that it is not a one to one function on its implied domain But if we limit the domain to \( ( \dfrac{\pi}{2} , \dfrac{\pi}{2} ) \), blue graph below, we obtain a one to one function that has an inverse which cannot be obtained algebraically
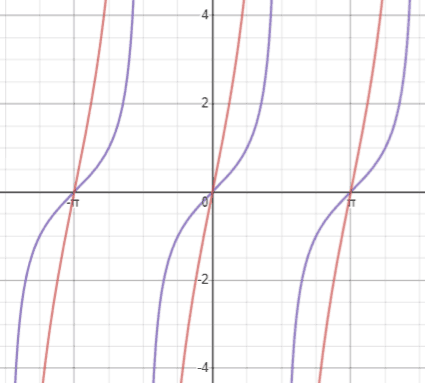


Tangent


Graphing Trig Functions Geogebra
That said, however, in your particular case, plotting both $\tan x$ and $2x$ will quickly show you there are more solutions One is the zero function, the other two can be only calculated numericallyMay 21, 12 · Get an answer for 'Tan^2(x)=3 Solve' and find homework help for other Math questions at eNotes(tan x)×(tan 2x) = 1 or tan x = 1/(tan 2x) =cot 2x or tan x = tan (pi/2 2x) or x = npi (pi/2–2x) or x2x= (n1/2)pi or 3x = (2n1)pi/2 or x = (2n1)pi



Graphing Tangent Read Trigonometry Ck 12 Foundation


Trigonometry Trigonometric Functions
Tan (90θ )= Cot θ;To calculate tan (2) degrees of a right angled triangle, we use the following equation where angle is 2 Tan(angle) = Opposite/Adjacent Tan 2 degrees is simply the ratio of the side opposite of the angle to the side adjacent to the angle As long as the angle stays at 2 degrees, the ratio does not change and tan 2 degrees is a fixed number See figure 1 for a better illustration The answer to "What is tan 2 degrees?"The trigonometric functions most widely used in modern mathematics are the sine, the cosine, and the tangentTheir reciprocals are respectively the cosecant, the secant, and the cotangent, which are less usedEach of these six trigonometric functions has a corresponding inverse function (called inverse trigonometric function), and an equivalent in the hyperbolic functions as well
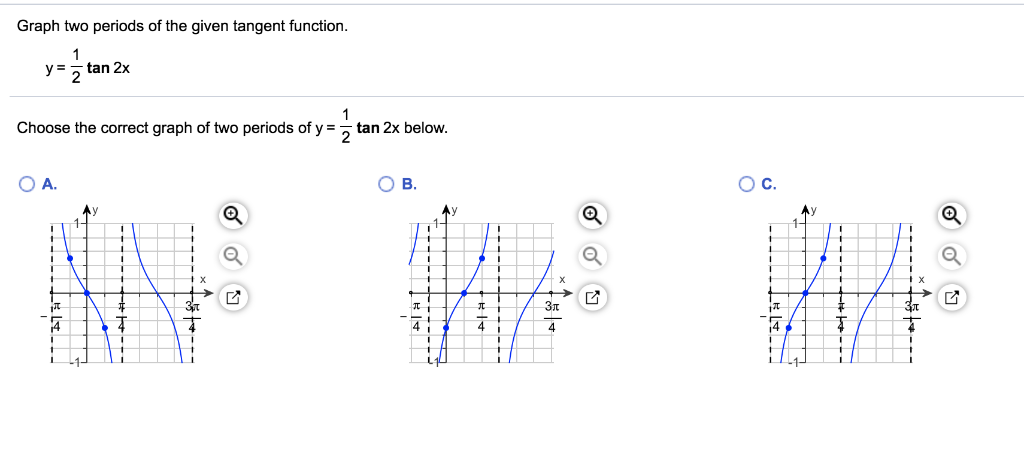


Solved Graph Two Periods Of The Given Tangent Function Y Chegg Com



Trigonometry Grade 11
21) sec 4 x tan 4 x = sec 2 x tan 2 x 21) Graph the expression on each side of the equals symbol to determine whether the equation might be an identity 22) sin θ 1 cos θ cot θ = tan θ 22) Use Identities to find the exact value 23) cos 75° 23) 24) cos π 12 24)Describe how to sketch the graph ofy = tan(2x) 3 using the parent function Start by graphing the tangent function Compress the graph horizontally by making the period onehalf pi Reflect the graph over the xaxis Shift the graph up 3 unitsTangent Function for Numeric and Symbolic Arguments Depending on its arguments, tan returns floatingpoint or exact symbolic results Compute the tangent function for these numbers Because these numbers are not symbolic objects, tan returns floatingpoint results



Weird Hidden Answer In 2 Tan 2x 3 Text Cot X Mathematics Stack Exchange
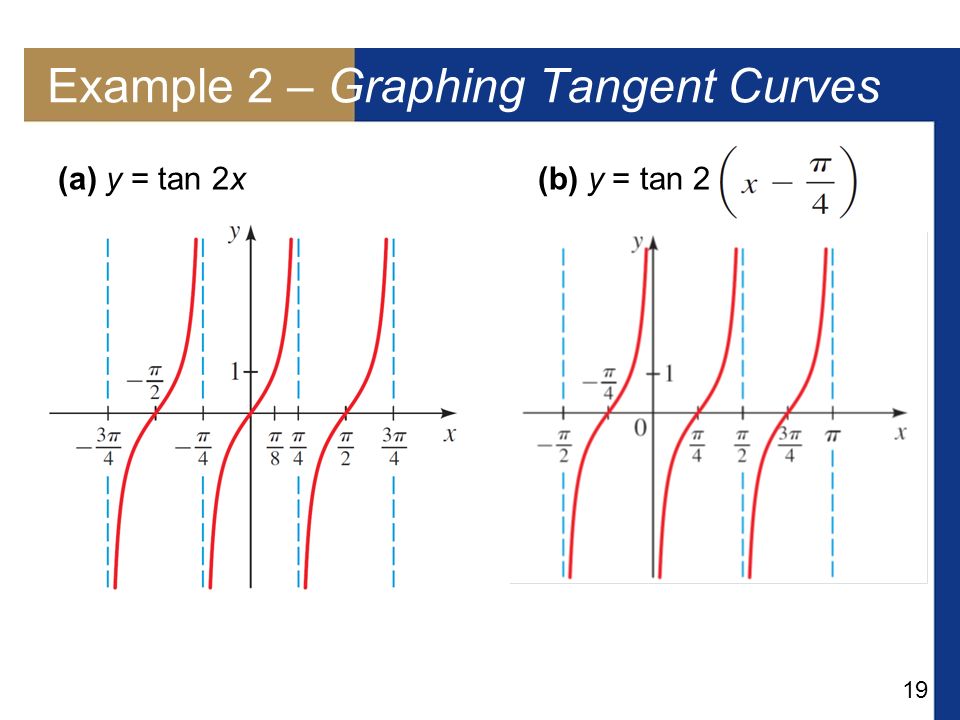


Tan2x ただの悪魔の画像
Tan 2x=2 tan x/1tan 2 x;Once you learn about the graphs of sine and cosine, its on to other trigonometric functions This video will show you the graphs of tangent and cotangentExampleFind the value of tan(9045)° Answer We know, tan(90θ )=cotθ ∴ tan(9045)=cot 45° And cot 45 0 =1 So, tan(9045)°=1 Example Show that tan 3xtan 2xtanx= tan 3xtan 2xtan x Answer We can write, 3x=2xx Alos, tan 3x= tan (2xx)
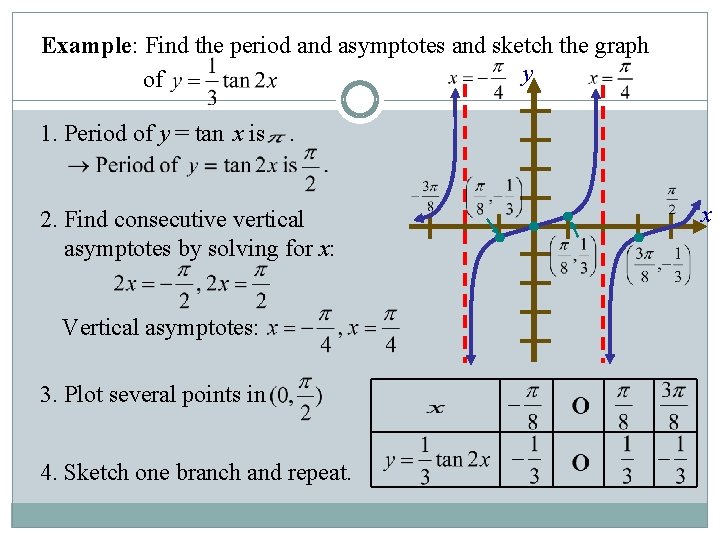


Unit 7 Trigonometric Functions Graphing The Trigonometric Function
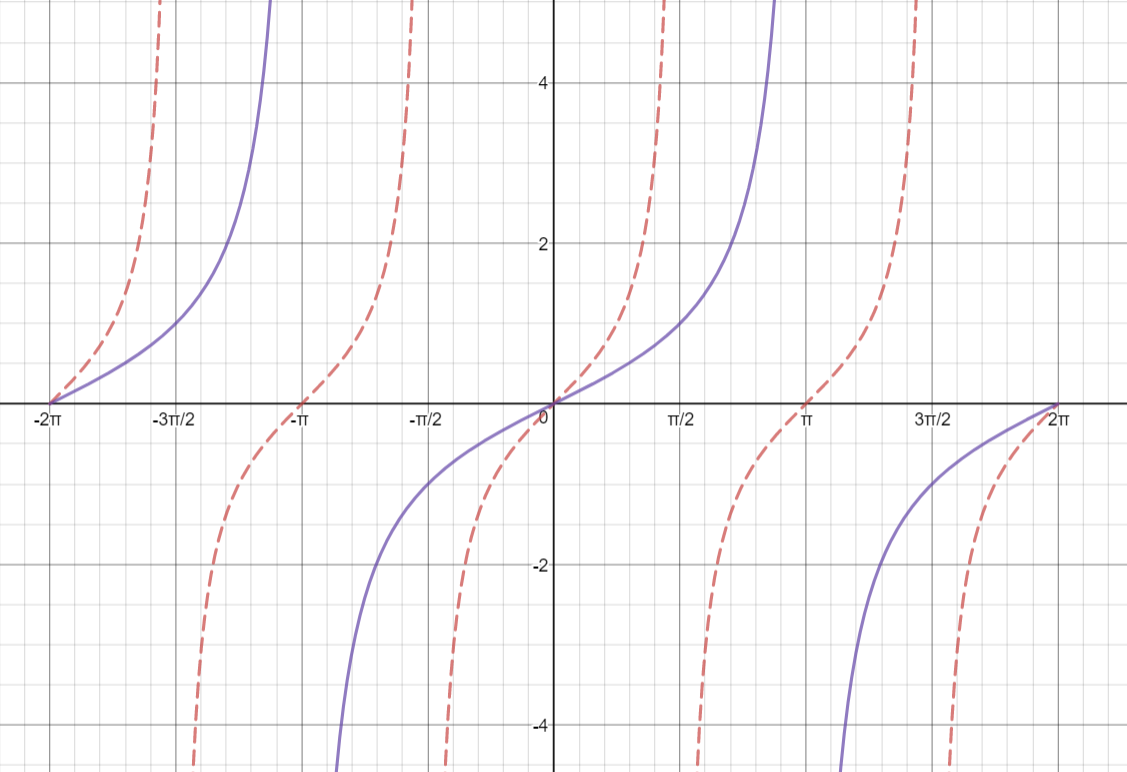


How Do You Graph Y Tan 1 2 X Socratic
Notation Several notations for the inverse trigonometric functions exist The most common convention is to name inverse trigonometric functions using an arc prefix arcsin(x), arccos(x), arctan(x), etc (This convention is used throughout this article) This notation arises from the following geometric relationships citation needed when measuring in radians, an angle of θHow to graph these two circular functions Tan and Cot cycle in 180 degrees not in 360 degrees Some of my favorite tools https//wwwamazoncom/shop/colfa16° to 31° 32° to 45° tangent (0°) = 0 tangent (16°) = tangent (32°) = tangent (1°) = tangent (17°) = tangent (33°) = tangent
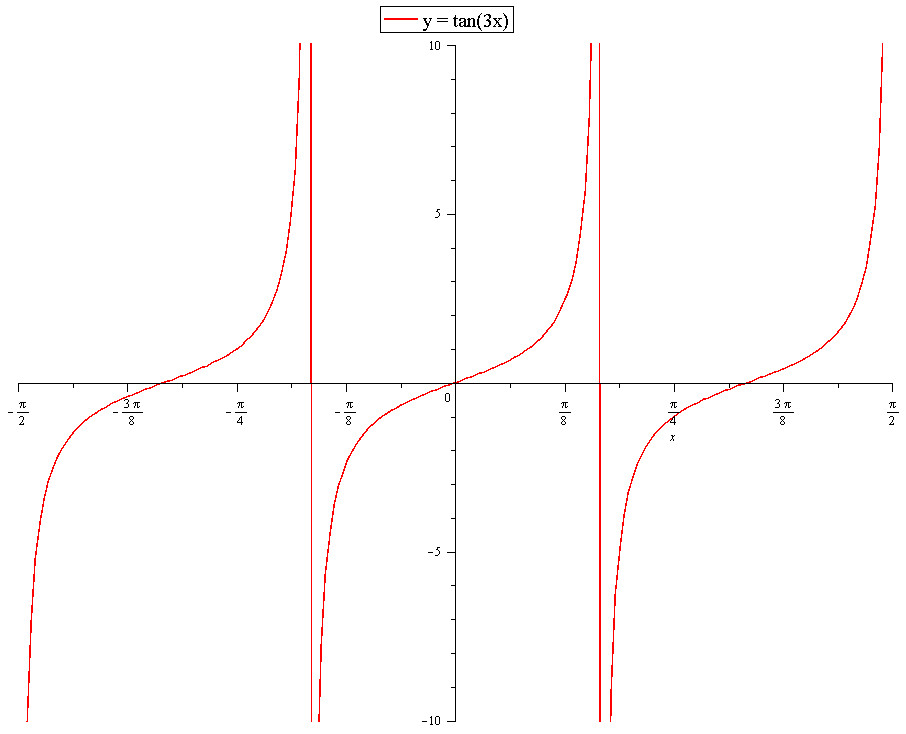


How Do You Graph Y Tan3x Socratic



Graphing Tangent Read Trigonometry Ck 12 Foundation
Precalculus Exponential and Logistic Functions Exponential and Logistic Graphs 1 Answer kubik98 Dec 23, 17 see below Explanation #f(x)=ln(tan^2x)# The Domain #uuu_(k in Z)(pi/2kpi, kpi)^^uuu_(k in Z)(kpi,pi/2kpi)# #f(x)=ln(tan(x))^2#



Tangent Graphs Worked Solutions Examples Videos



Graphs Of Trigonometric Functions


4 Graphs Of Tan Cot Sec And Csc
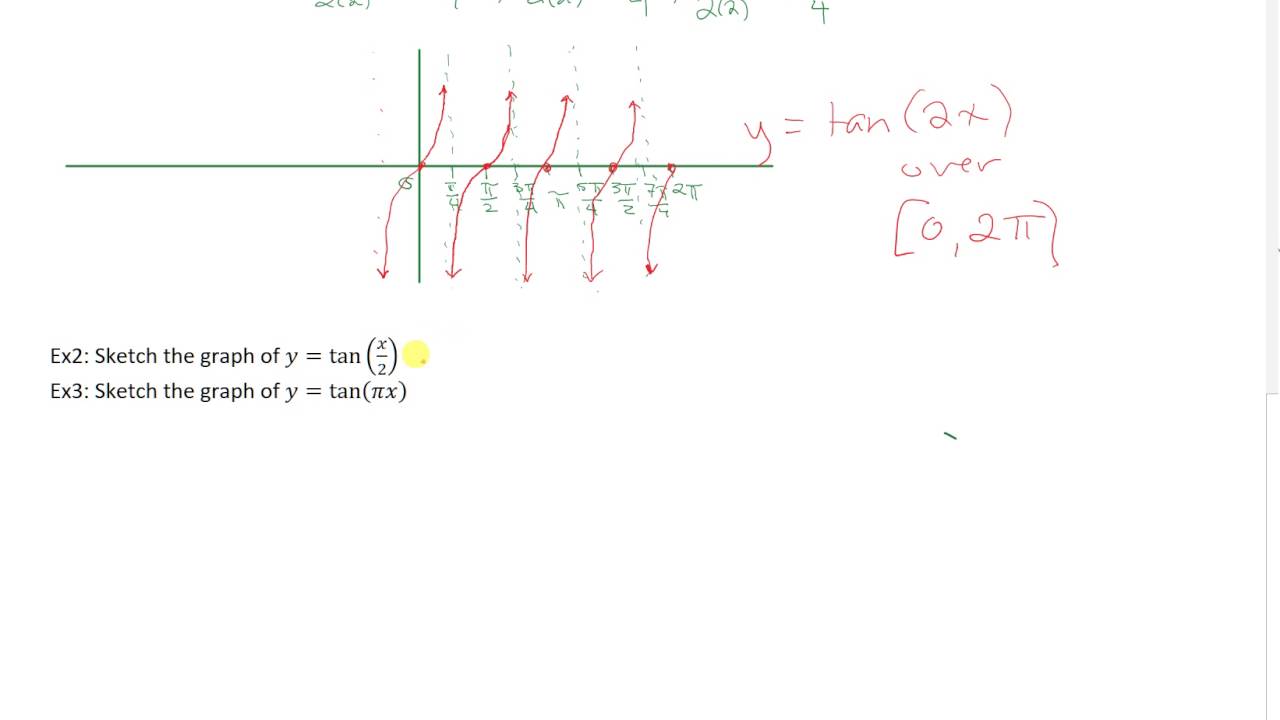


Sketching Y Tan 2x And Y Tan X 2 Youtube
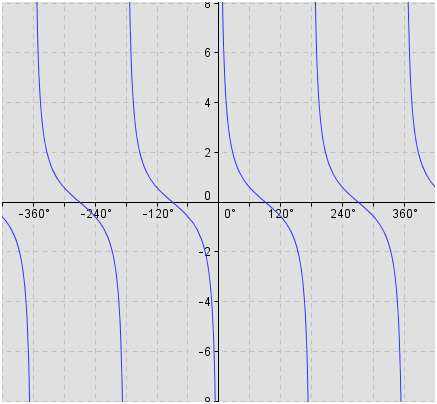


Trigonometry Trigonometric Functions
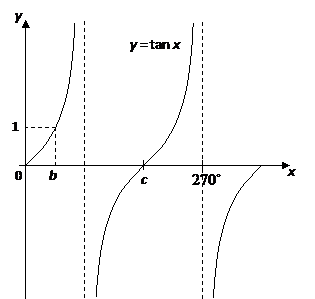


Tangent Graphs Worked Solutions Examples Videos


How Do You Graph Y Tan X 90 Socratic



The Tangent Function Functions Siyavula



Trigonometry Grade 11



Graphing The Tangent Function Amplitude Period Phase Shift Vertical Shift Video Lesson Transcript Study Com


Tangent Cotangent Secant And Cosecant Graphs Mathbitsnotebook Ccss Math


Tangent Graphs


Trig Graphs And Equations Ppt Download


What Is The General Solution Of X For Tan X Tan2x 1 Quora



Trigonometry Reciprocal Identities Expii
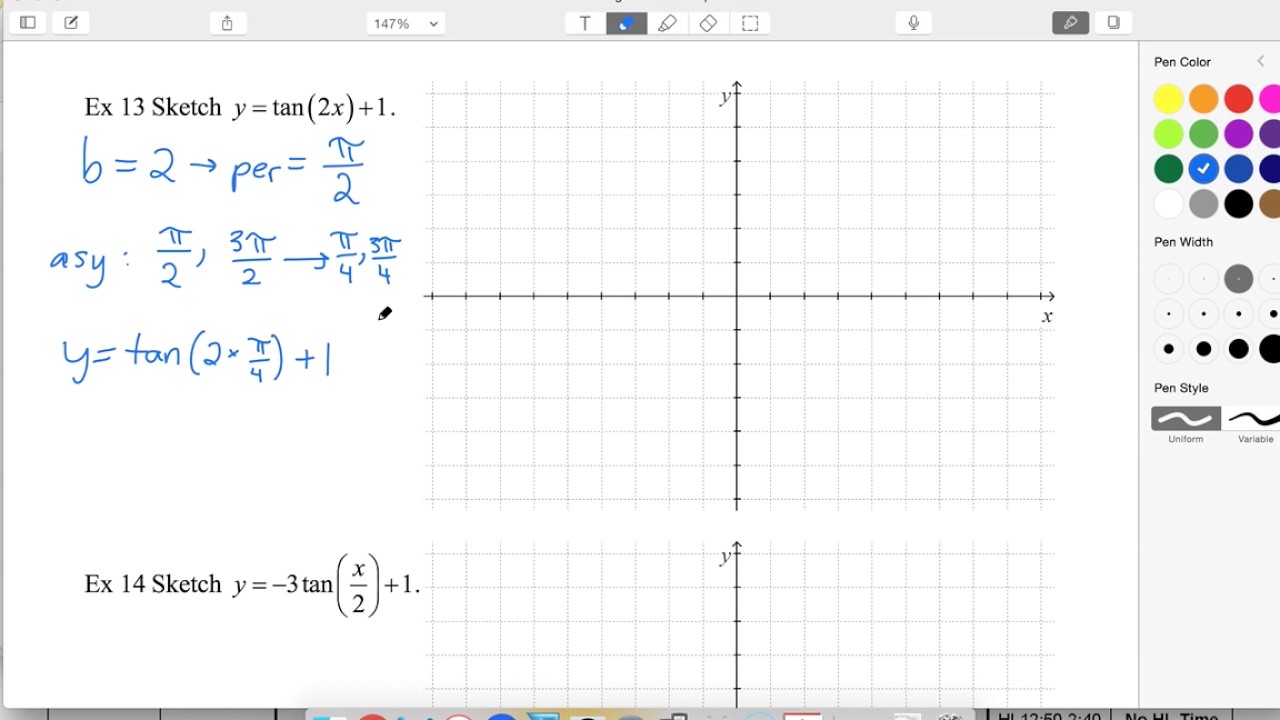


01 Ex13 Sketch Y Tan 2x 1 Youtube


Trigonometry Trigonometric Functions



Trig Graphs Investigate The Effects Of 2sin X 2cos X 2tan X Ppt Video Online Download


Solution How To Find The Number Of Cycles In 2pi The Horizontal Length Of Each Of The 4 Quadrants Of Each Cycle The Horizontal Shift Of Each Cycle F X Tan 2x 3


Content Graphing The Trigonometric Functions


Sine Cosine Tangent Graphs Video Lessons Examples And Solutions



The Tangent Function Functions Siyavula


How To Calculate The Area Under The Graph Tan X Between 0 And Pi 2 Quora



The Tangent Function Functions Siyavula


Python Math Tan Function Geeksforgeeks


Content Graphing The Trigonometric Functions
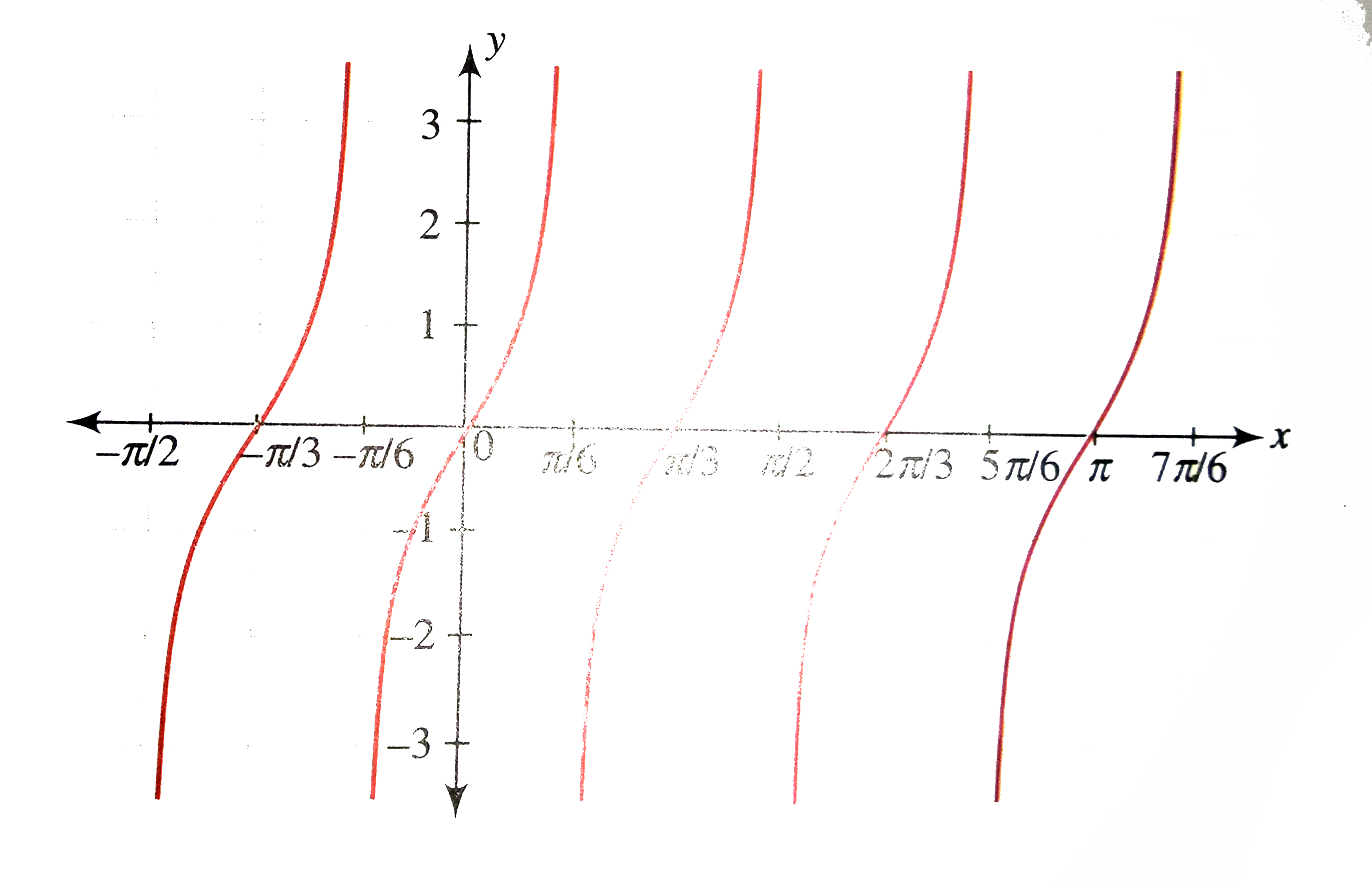


Draw The Graph Of Y Tan 3x


Solved 1 Carefully Sketch The Graph Of Y Tan X Over 1 Chegg Com



Sketch The Graph Of The Tangent Curve Y Tan 2x In The Interval From 0 To 2pi Brainly Com


Biomath Trigonometric Functions
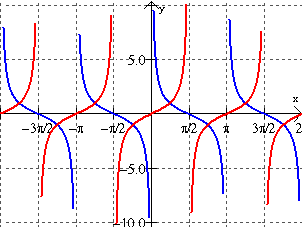


Tangent Cotangent Secant And Cosecant Graphs Mathbitsnotebook Ccss Math


Solution Determine The Period Of Y Tan 2x
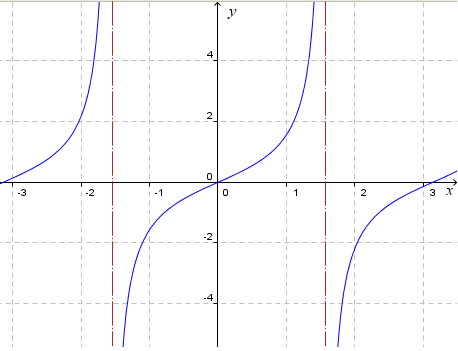


Explore The Slope Of The Tan Curve


Solution Show Me The Graph Of Y Tan2x Step By Step And How To Solve Keypoints


Find The Period Of Tan 2x Class 10 Maths Cbse


How Do You Graph Y Tan3x Socratic


Arctan


Tan Graph



How To Graph Tan Ex Y Tan2x Study Com



Graphing Tangent Read Trigonometry Ck 12 Foundation


Solution Consider The Graph Of Y Tan X A How Does It Show That The Tangent Of 90 Degrees Is Undefined B What Are Other Undefined X Values C What Is The Value Of


Graph Tangent And Cotangent
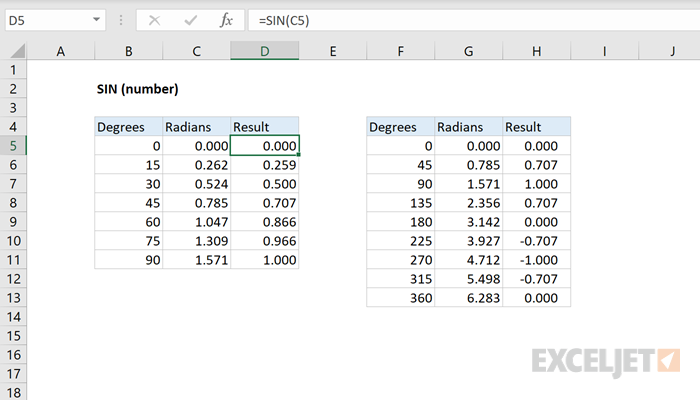


How To Use The Excel Sin Function Exceljet
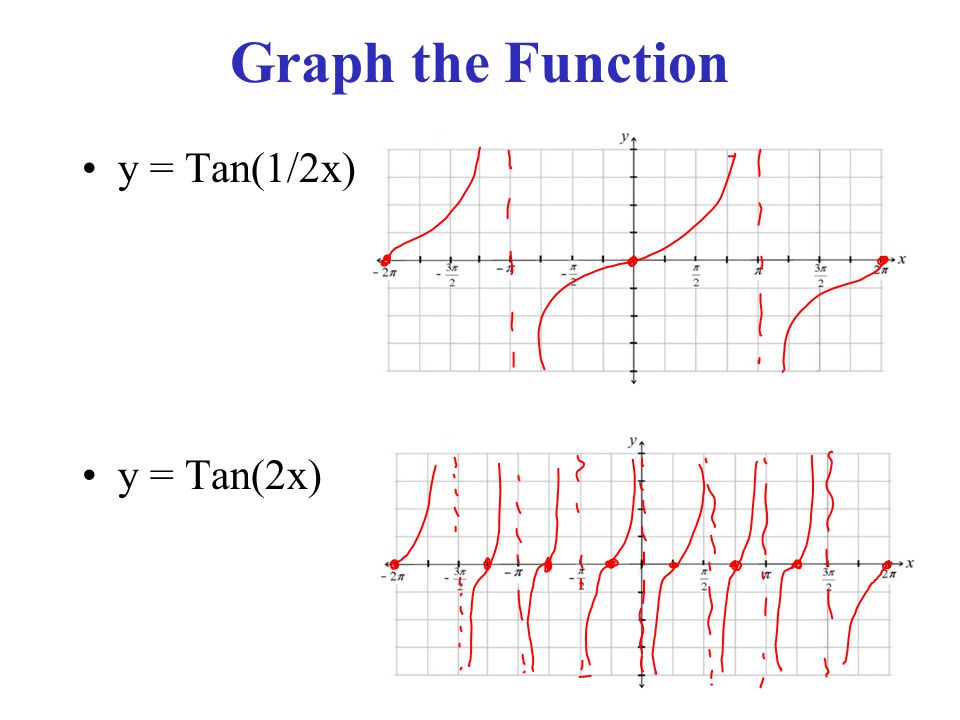


Warm Upnov 25 Th Determine Whether To Us The Law Of Sine Or Cosine And Solve For The Missing Pieces 1 D Abc With A 12 B 13 C 24 2 D Abc Ppt Download
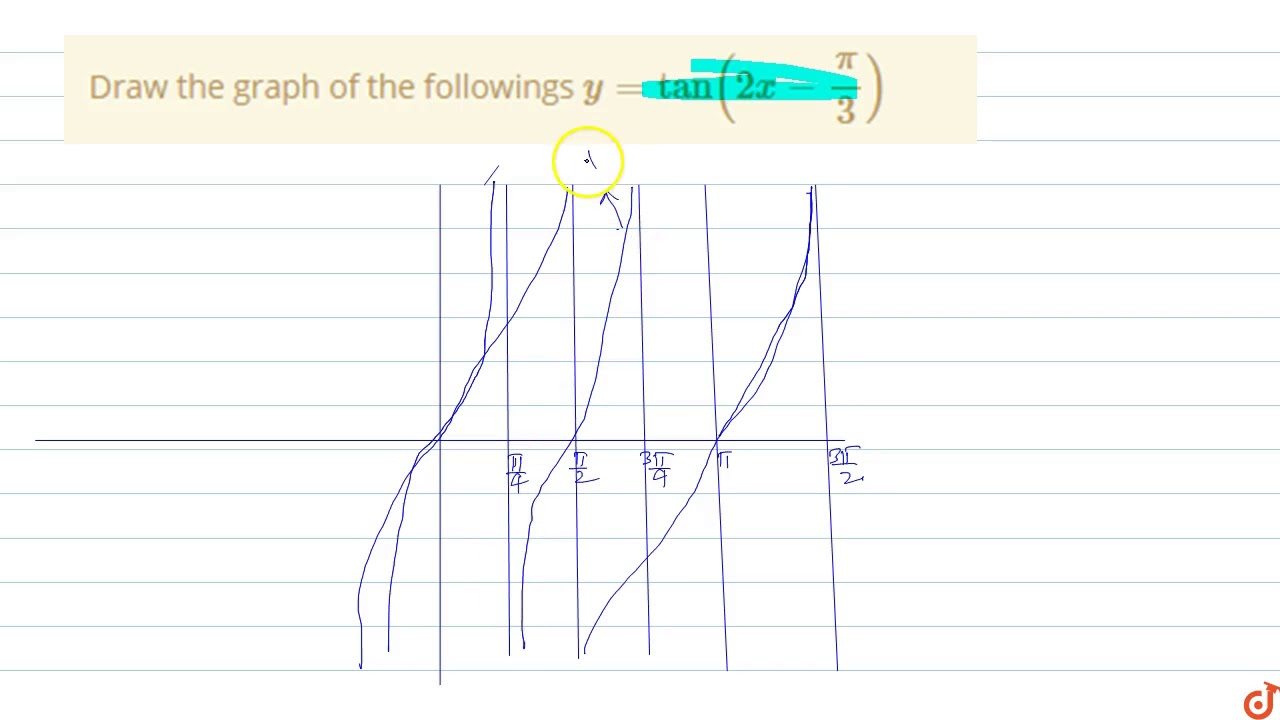


Draw The Graph Of The Followings Y Tan 2x Pi 3 Youtube


Bestmaths
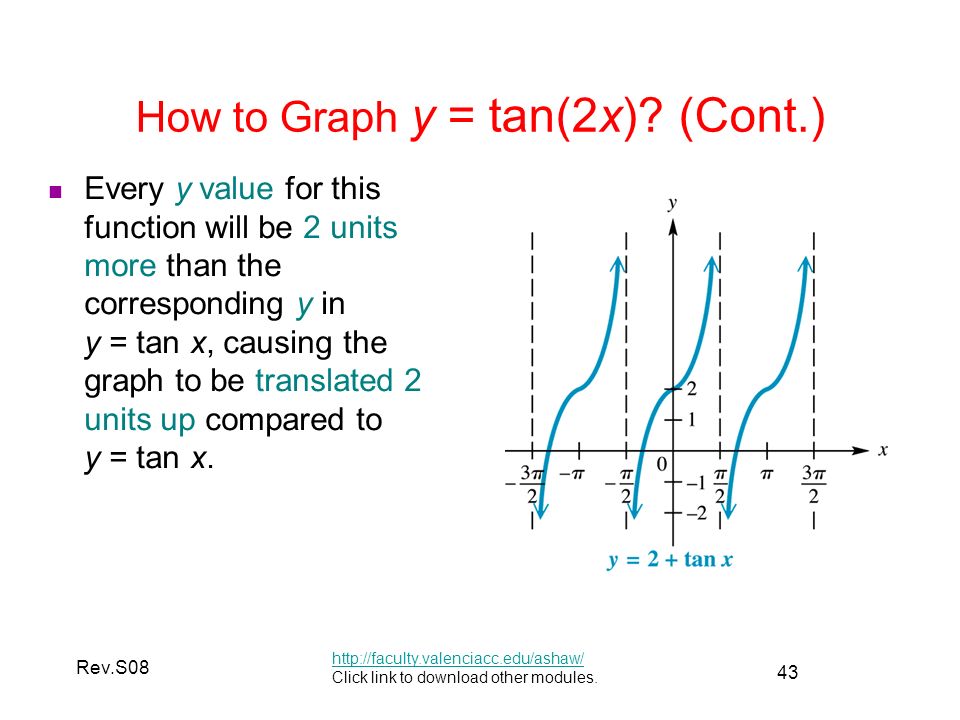


Rev S08 Mac 1114 Module 4 Graphs Of The Circular Functions Ppt Download


Inverse Trigonometric Functions Precalculus Ii
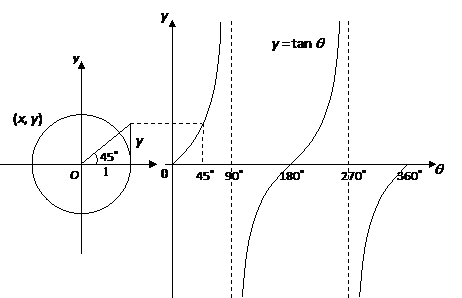


Tangent Graphs Worked Solutions Examples Videos



Solved Find The Period And Graph Two Cycles Of Y Tan 2x Chegg Com
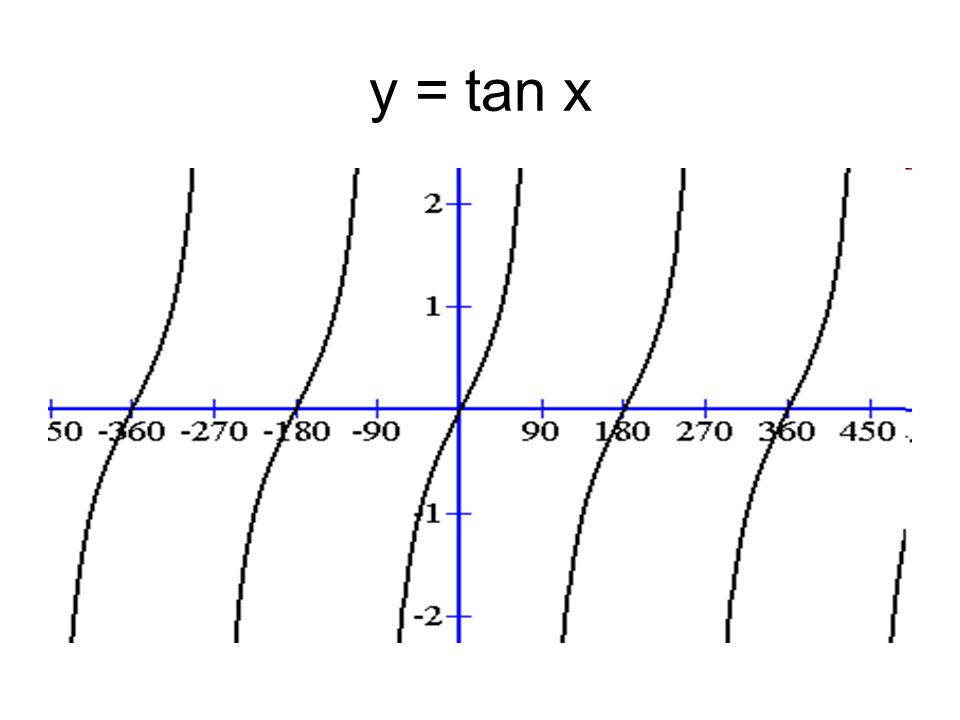


Trig Graphs Y Sin X Y Cos X Y Tan X Y Sin X Ppt Download



Trigonometric Functions Ppt Video Online Download


How To Get A Perfect Tan Graph Mr Modolo S Mhf 4u Class Site



Graphing Tangent Read Trigonometry Ck 12 Foundation


Cofunction Calculator


Trigonometry
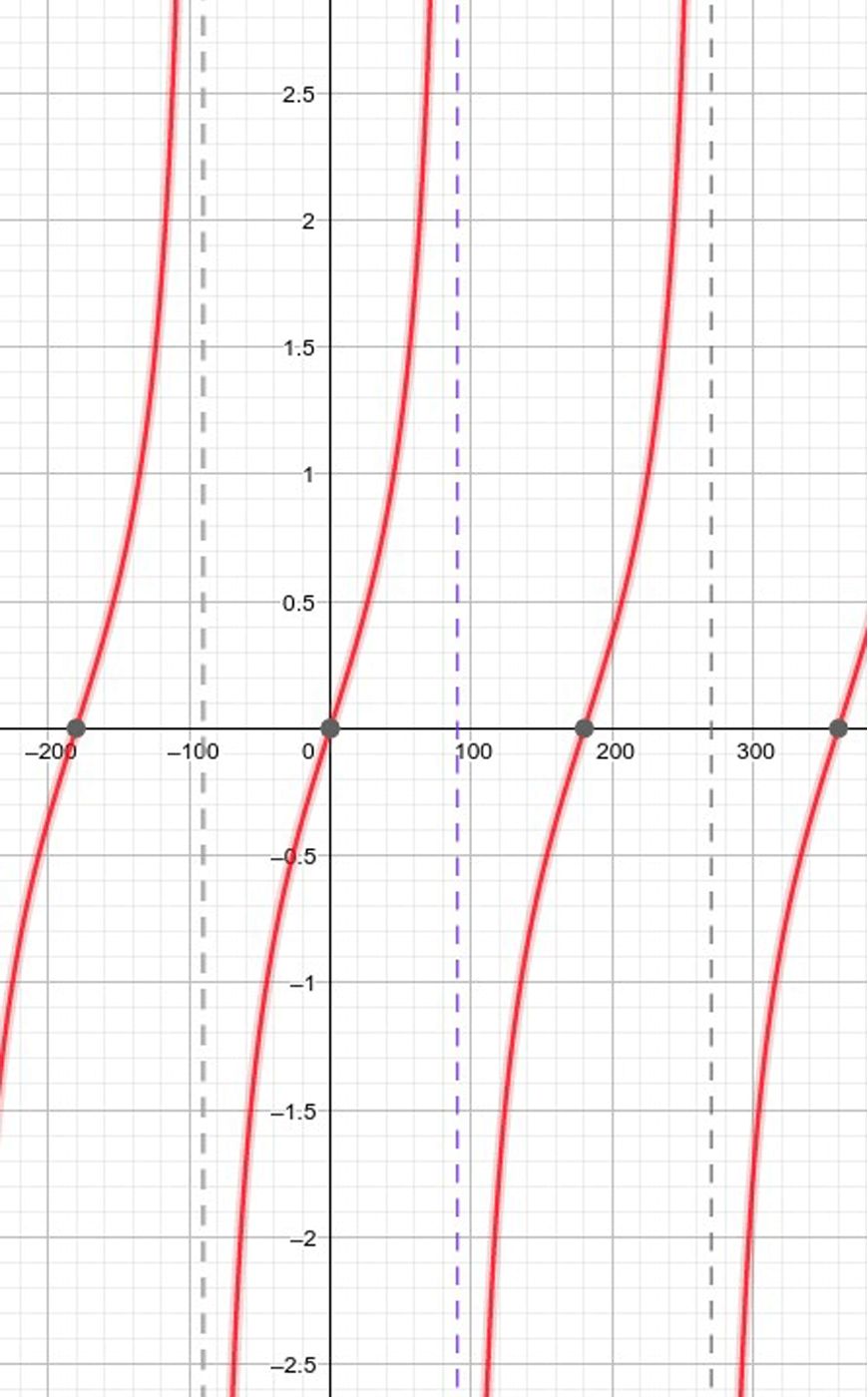


Part 4 Year 10 Further Trigonometry Applications Year 10 Maths Guide



Symbolic Tangent Function Matlab Tan


Solution Graph Y 1 2 Tan 2x Pi 2 And The Period And Phase Shift


Tangent Graphs
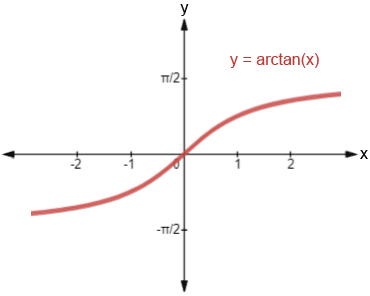


Arctan



Identities S Cool The Revision Website



Graphing The Tangent Function Amplitude Period Phase Shift Vertical Shift Video Lesson Transcript Study Com


4 Graphs Of Tan Cot Sec And Csc



Trigonometric Functions



What Are The Solutions For X Tan X Quora


Inverse Trigonometric Functions Precalculus Ii



Trigonometric Functions



Mathematics 10 Graphing Periodic Functions Daiki Yamamoto S



0 件のコメント:
コメントを投稿